1. 문제
https://www.acmicpc.net/problem/1753
2. 풀이 과정
이 문제는 방향 그래프와 시작점 K가 주어진다. 시작점에서 출발해 다른 모든 정점까지의 최단 경로를 구하는 문제이다.
경로가 존재하지 않으면 INF를 출력한다.
이 문제는 다익스트라(Dijkstra) 알고리즘을 활용하는 가장 기본적인 문제이다.
다익스트라 알고리즘
가중치가 있는 그래프에서 하나의 시작점으로부터 다른 모든 정점가지의 최단 거리를 구하는 알고리즘이다.
항상 현재까지 발견된 최단 경로 중 가장 짧은 경로부터 확정해 나가는 방식이다.
동작과정
- 시작 노드의 최단 거리를 0으로 설정, 다른 모든 노드는 INF로 초기화
- 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드 선택
- 그 노드를 거쳐서 다른 노드로 가는 비용을 계산하고, 기존 비용보다 짧으면 갱신
- 모든 노드가 방문될 때까지 2, 3번 과정을 반복
풀이 예시
입력
5 6
1
5 1 1
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6
문제 입력에 대한 그래프 형태는 다음과 같다.
정점:1~5
간선 개수: 6개
시작 정점: 1
정점 간 방향과 가중치(w)를 가진다.
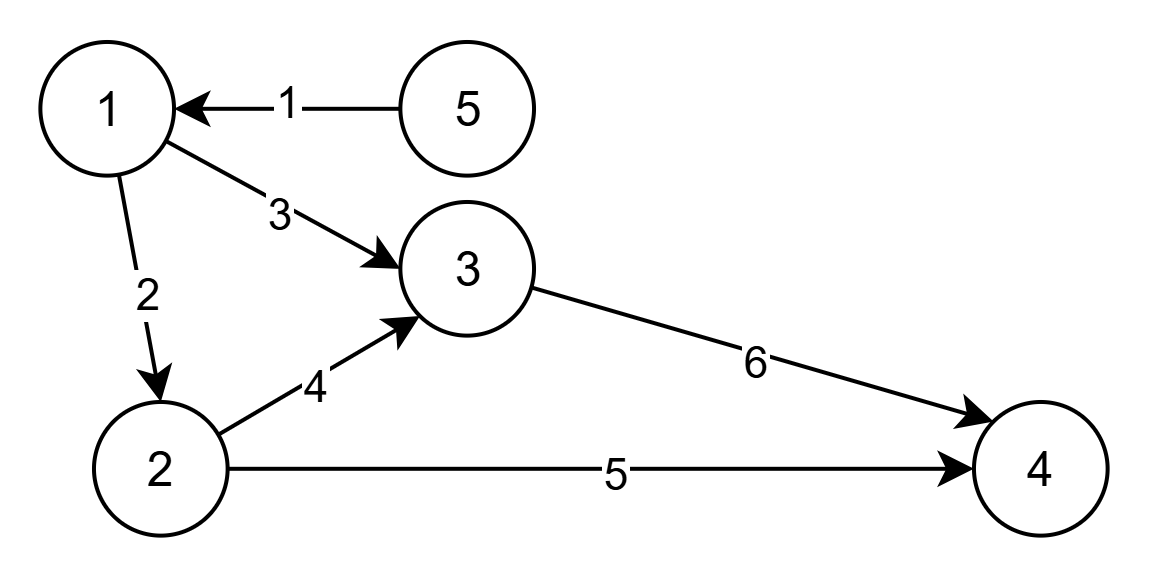
각 정점에 대한 최단 거리를 저장하는 배열 result를 INF로 초기화 한다.
result의 index는 정점까지의 거리를 뜻한다. index = 1~5
[INF, INF, INF, INF, INF]
1. 시작점(1): result[1] = 0
- result = [0, INF, INF, INF, INF]
2. 1번 정점과 연결된 정점 갱신
- 1 -> 2 (w=2)
- 1 -> 3 (w=3)
- result = [0, 2, 3, INF, INF]
3. 2번 정점과 연결된 정점 갱신
- 2 -> 3 (기존 3 vs 2 + 4 = 6 -> 유지)
- 2 -> 4 (2 + 5 = 7)
- result = [0, 2, 3, 7, INF]
4. 3번 정점과 연결된 정점 갱신
- 3 -> 4 (기존 7 vs 3 + 6 = 9 -> 유지)
- result = [0, 2, 3, 7, INF]
5. 4번 연결된 정점 갱신
- 4번과 연결된 정점 없음.
- 5번 정점은 시작점에서 도달 불가 -> INF 유지
6. 최종 결과
- result = [0, 2, 3, 7, INF]
3. 코드
- 최단 거리를 가진 정점을 빠르게 뽑기 위해 우선순위 큐를 사용한다.
- 이미 확정된 정점은 다시 처리하지 않도록 visited 배열 사용
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static int V;
static int E;
static int K;
static List<List<Point>> graph = new ArrayList<>();
static int[] result;
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
K = Integer.parseInt(br.readLine());
result = new int[V + 1];
for (int i = 0; i <= V; i++) {
graph.add(new ArrayList<>());
result[i] = Integer.MAX_VALUE;
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
graph.get(u).add(new Point(v, w));
}
dijkstra();
for (int i = 1; i <= V; i++) {
if (result[i] == Integer.MAX_VALUE) {
bw.write("INF\n");
} else {
bw.write(result[i] + "\n");
}
}
bw.flush();
bw.close();
}
static void dijkstra() {
PriorityQueue<Point> pq = new PriorityQueue<>((o1, o2) -> o1.w - o2.w);
boolean[] visited = new boolean[V + 1];
pq.offer(new Point(K, 0));
result[K] = 0;
while (!pq.isEmpty()) {
Point cur = pq.poll();
if (visited[cur.x]) {
continue;
}
visited[cur.x] = true;
for (Point next : graph.get(cur.x)) {
if (result[next.x] > result[cur.x] + next.w) {
result[next.x] = result[cur.x] + next.w;
pq.add(new Point(next.x, result[next.x]));
}
}
}
}
static class Point {
int x;
int w;
public Point(int x, int w) {
this.x = x;
this.w = w;
}
}
}
'Algorithm' 카테고리의 다른 글
| [백준] 1238.파티 - Java (0) | 2025.09.29 |
|---|---|
| [백준] 1504. 특정한 최단 경로 (0) | 2025.09.25 |
| [백준] 13460. 구슬 탈출2 - JAVA (0) | 2025.09.18 |
| [백준] 14502. 연구소 - JAVA (0) | 2025.09.16 |
| [백준] 3190. 뱀 -JAVA (0) | 2025.09.14 |